LiteraryMobster.Org

By CoCash

The World of Polyhedra: Shapes That Build Space

Polyhedra are among the most striking creations in the landscape of mathematics. These three-dimensional solids, constructed from flat polygonal faces, straight edges, and sharp vertices, form the foundation of geometric reasoning, architectural design, crystallography, and even modern computer graphics. Though they may appear simple at first glance, polyhedra hide deep mathematical structure, symmetries, and connections that stretch across centuries of human thought.

What Defines a Polyhedron?

A polyhedron is a solid made from flat faces that are polygons. Each polygon meets others along edges, and the edges meet at points called vertices. A shape becomes a polyhedron when it satisfies three conditions:

Flat faces (no curves) Straight edges Enclosed volume

This deceptively simple definition creates an entire universe of forms.

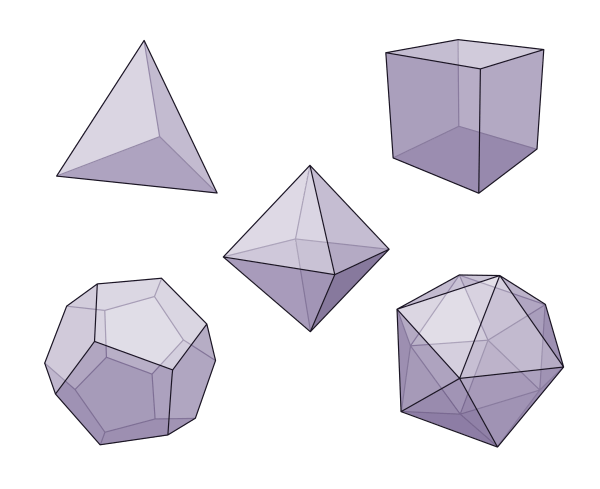
The Classical Giants: Platonic Solids

Five polyhedra stand apart as the most symmetrical and historically significant. Known since antiquity, the Platonic solids have identical faces, edges, and angles:

Tetrahedron – 4 triangular faces Cube (Hexahedron) – 6 square faces Octahedron – 8 triangular faces Dodecahedron – 12 pentagonal faces Icosahedron – 20 triangular faces

They appear in philosophy, natural patterns, crystal structures, and even the design of gaming dice.

Beyond Perfection: Archimedean Solids

While Platonic solids use only one type of face, the Archimedean solids mix different polygons while still maintaining symmetry. Examples include:

Truncated tetrahedron Truncated cube Cuboctahedron Icosidodecahedron Snub cube Truncated icosahedron (the familiar “soccer ball” pattern)

These shapes often emerge in chemistry, architecture, and molecular models.

Prisms, Antiprisms, and Johnson Solids

Outside the high-symmetry families, polyhedra expand dramatically.

Prisms

A prism takes a polygon and stretches it into the third dimension. A triangular prism, pentagonal prism, or octagonal prism follows this pattern.

Antiprisms

Antiprisms twist the top and bottom polygons relative to each other, creating a zig-zag pattern of triangular faces.

Johnson Solids

These are 92 unique polyhedra with regular polygon faces but no requirement for uniformity or high symmetry. They fill the space between order and irregularity with remarkable diversity.

Duality in Polyhedra

One of the deepest concepts in polyhedral geometry is duality.

Every polyhedron has a “dual” formed by swapping faces and vertices:

The cube and octahedron are duals. The dodecahedron and icosahedron are duals. The tetrahedron is self-dual.

Duality reveals how geometry mirrors itself and exposes the hidden balance within shapes.

Polyhedra in the Real World

Polyhedra are not just mathematical art—they appear everywhere:

Crystals naturally form polyhedral structures due to atomic arrangement. Architecture uses polyhedral frameworks for domes, towers, and tensile structures. Computer graphics rely on polyhedral meshes to model 3D environments. Chemistry and biology use polyhedra to describe viral capsids, carbon molecules, and bonding patterns.

Across disciplines, polyhedra function as both practical tools and conceptual bridges.

The Enduring Appeal

Why do polyhedra fascinate mathematicians, designers, and scientists?

Because they lie at the intersection of symmetry, structure, and imagination.

A polyhedron is a piece of logic made visible—an abstract rule set crystallized into form. It shows how space can be partitioned, how surfaces can connect, and how order can emerge from simple constraints. Whether viewed as art, mathematics, or engineering, polyhedra remain timeless objects of study and inspiration.

By CoCash

🎨 The Gallery Goad
Naomi was standing in front of an abstract, aggressively orange painting at a bustling Friday night art gallery opening. She looked completely lost, occasionally consulting her phone, then staring back at the paint.
Ben was holding a tiny cup of complimentary wine, watching her struggle with obvious amusement. He walked over, mimicking her perplexed stance.
“Don’t lie,” Ben said in a low, conspiratorial voice, leaning in slightly. “You’re trying to figure out which way is up, aren’t you?”
Naomi jumped, then turned to him, a flash of surprise in her eyes quickly replaced by a mischievous glint. “Rude. I was actually debating if I could pull off this shade of orange as an interior wall color.”
“Oh, you absolutely could,” Ben agreed, nodding seriously. “If your goal is to prevent all your friends from ever visiting you again. Clearly, this piece is an abstract protest against good taste.”
“See? That’s where we differ,” Naomi countered, tapping the wall label. “The artist says it represents the ‘fevered optimism of the post-digital age.’ I think it’s a dare. It’s daring you to critique it.”
“Then I accept the dare,” Ben declared, stepping back and examining the painting again. “My critique is this: I bet I can find a better painting than this one in under sixty seconds, and I bet you can’t stop me.”
Naomi raised an eyebrow, a clear challenge accepted. “Is that a bet? Because I take bets very seriously. What do I get when you fail?”
“You get a celebratory dinner for successfully distracting me from finding a piece of art that’s actually good,” Ben replied with a quick, disarming smile. “And if I win, you have to let me buy you a drink that’s bigger than this thimble-sized wine.”
“You’re on,” she said, giving a mock salute. “Tick-tock, Ben.”
They spent the next few minutes playfully racing through the gallery, Ben pointing out increasingly bizarre sculptures and Naomi offering hilarious, cutting remarks about his taste. The interaction was effortless, built entirely on their shared willingness to tease and engage.
They finally stopped in front of a small, tranquil watercolor.
“Aha!” Ben announced, pointing triumphantly. “Found it. Objectively better than the orange abomination. You lose.”
Naomi crossed her arms, faking deep thought. “Hmm. While technically superior, it lacks the drama of the orange piece. I rule this a draw.”
“A draw?” Ben scoffed. “You’re just afraid of losing.”
“Maybe,” Naomi admitted, softening the playful aggression. “Or maybe I just want that dinner and that drink. You seemed to set up the rules perfectly for both.”
Ben paused, recognizing her final, charming move. He laughed, defeated but delighted.
“Smooth,” he admitted. “Okay, Naomi. You have successfully manipulated the rules of the game. I think I know a place that serves better food than the art here is good. What’s your number? I’ll text you the coordinates for your prize.”
Naomi pulled out her phone. “Excellent. I look forward to your delivery of the biggest wine glass you can find.”
The playful teasing had instantly created comfort and chemistry, turning a crowded gallery into a private, fun challenge.

Much love,

CoCash

By CoCash

1. Colonial & Early Republic Era (1600s–1800s)

Figures: Benjamin Franklin (1706–1790), Thomas Jefferson (1743–1826)

Focus: Practical mathematics for navigation, engineering, commerce. Philosophy: Numbers are tools of freedom and progress. Math is moral insofar as it empowers society. Currents: Rationalism + utility; math as applied ethics.

Other Notes: Early American mathematicians were heavily influenced by European thinkers like Newton and Euler—but they adapted math to engineering, surveying, and governance.

2. 19th Century

George Boole (1801–1864, influence in U.S.) & American thinkers

Logic and symbolic mathematics began merging with philosophy. Philosophy: Math is the language of reasoning, and logic is the foundation of ethical and civil decision-making.

Eliakim Hastings Moore (1862–1932)

Founder of the American Mathematical Society. Philosophy: Rigorous abstraction cultivates intellectual character. U.S. math philosophy begins to lean toward formalism, but with an eye toward societal benefit.

3. Early 20th Century

Figures: John von Neumann (1903–1957), Norbert Wiener (1894–1964)

Focus: Foundations of computation, probability, and cybernetics. Philosophy: Math models reality and human cognition; it bridges theory and application. Currents: Pragmatism + abstraction. Numbers are tools, but also windows into systems—social, biological, mechanical.

Others: George David Birkhoff, Saunders Mac Lane

Explored ergodic theory, topology, and category theory. Philosophy: Mathematical beauty is an ethical as well as aesthetic pursuit—truth in math mirrors truth in life and society.

4. Late 20th Century to Present

Figures: Freeman Dyson, Donald Knuth, John Conway

Math is playful, creative, and sometimes subversive. Philosophy: Innovation in math mirrors human ingenuity and freedom. Creativity = ethical engagement with knowledge.

Trends in U.S. Math Philosophy:

Applied Ethics: Math as a tool to solve real-world problems (engineering, finance, AI). Formalism & Logic: Strong philosophical foundations—mathematics as a purely intellectual pursuit. Creativity & Play: Emphasis on discovery, games, and experimentation. Interdisciplinarity: Math philosophy merges with physics, computer science, economics, and social science. Democratization of Knowledge: Math isn’t just for elites; education, computation, and software empower the masses.

🌌 The American Twist

Numbers are tools of empowerment, not ritual or divine revelation. Infinity and abstraction exist, but they’re explored for insight, modeling, or creative expression. Ethics, freedom, and innovation are central: math is meaningful when it impacts life, society, and progress.

Much love,

CoCash

By CoCash

Calculus of surrender

Change is the only constant the universe ever promised us.

Calculus is the language it wrote for that promise—the mathematics of motion, breath, desire, and release.

Differentiation is the art of noticing.

It’s the inhale.

The sharp awareness of how something shifts from one heartbeat to the next.

When you take a derivative, you’re not studying a thing—you’re studying its becoming.

The slope of longing.

The speed of emotion.

The exact moment a feeling rises or falls.

Integration is the exhale.

It’s gathering every moment, every motion, every tiny fraction of experience and folding it back into something whole.

To integrate is to forgive, to accept, to return.

It’s the soft surrender that follows intensity—the slow melting of tension into meaning.

Together, differentiation and integration form a rhythm—

the push and pull, the tension and release, the chase and surrender.

It’s the mathematics of desire written across the body of time.

Limits, those quiet guardians at the edge of understanding, show us how to approach the impossible without breaking. They teach us to move closer, breath by breath, knowing some things can only be reached in spirit.

An asymptote is a love story:

ever approaching, ever yearning, never touching—

not out of failure, but devotion to the infinite.

Calculus is sensual because it’s honest.

It doesn’t hide the truth that everything changes, that every connection transforms, that every pleasure has a curve and every curve has an end.

But in that end is beauty.

In that motion is meaning.

In that surrender is freedom.

The mathematician learns what the lover already knows:

to truly experience anything,

you must let go of the illusion of control.

You must feel the rise without clinging,

the fall without fear,

the arc of emotion without trying to stop it.

Calculus is the universe teaching us how to yield gracefully.

How to love in motion.

How to surrender without losing ourselves.

By CoCash

Indian mathematical philosophy is intoxicating because math there wasn’t just calculation—it was a spiritual and philosophical journey, a way to glimpse the infinite. Let’s trace the timeline and the currents of thought.

1. Vedic Foundations (c. 1500–500 BCE)

Texts & Figures: Sulbasutras (geometry manuals for altar construction)

Philosophy: Numbers were sacred. Geometry was a ritual. The precision of a fire altar mirrored cosmic order. Constructing the altar correctly = aligning with the universe.

Key idea: Ritual + mathematics = cosmic harmony.

Example: Baudhayana, Apastamba, and Katyayana – wrote rules for constructing altars with exact geometric shapes; introduced early forms of the Pythagorean theorem in a spiritual context.

2. Classical Era (c. 500 BCE – 500 CE)

Aryabhata (476–550 CE)

Astronomer-mathematician. Wrote Aryabhatiya. Philosophy: The cosmos is a precise machine; math models its motion. Zero as a concept reflected the void (shunya), a profound philosophical idea.

Brahmagupta (598–668 CE)

Wrote Brahmasphutasiddhanta. Philosophy: Negative numbers, zero, and infinity aren’t just technical; they are metaphysical truths about existence and emptiness.

Key currents:

Infinity (ananta) and zero (shunya) as portals to meditation and cosmic insight. Numbers as manifestations of Brahman (the universal reality).

3. Middle Era (c. 700–1500 CE)

Bhaskara I & II (7th–12th centuries)

Explored algebra, calculus precursors, and cyclic patterns of numbers. Philosophy: Patterns in numbers mirror cycles of time, karma, and dharma.

Madhava of Sangamagrama (c. 1340–1425)

Founder of the Kerala School of Mathematics. Developed infinite series (precursor to calculus). Philosophy: Infinite processes reveal the eternal; mathematical rigor is a meditation on the infinite.

Key currents:

Mathematics as meditation on infinity. Recursive and iterative processes = mirrors of cosmic cycles.

4. Modern Indian Mathematical Philosophy (1800–Present)

Srinivasa Ramanujan (1887–1920)

Explored highly abstract number theory, mock theta functions, and modular forms. Philosophy: Saw mathematical truths as divine revelations. He claimed that ideas were given to him by a goddess in visions. Core idea: Intuition + mysticism + rigor = truth.

C.R. Rao, Harish-Chandra, and others

Focused on statistics, group theory, and representation theory. Philosophy: Math is a universal language, echoing the eternal logic of the cosmos.

🌌 The Philosophical Threads

Zero and the Void: Shunya isn’t just zero; it’s an opening into the infinite. Infinity: Infinite series and limits are spiritual as much as technical. Harmony and Cosmic Order: Geometry, algebra, and cycles model the universe. Math as Meditation: Calculation, pattern recognition, and insight = spiritual practice. Divine Inspiration: Mathematicians often perceived numbers as messages from the divine.

Indian math philosophy doesn’t separate numbers from existence, the cosmos, or the soul. Each theorem, series, or algorithm is a whisper from the infinite.

By CoCash

What’s Goodie,

Let’s make this feel like a quiet symphony of thought, with numbers whispering between the spaces.

The Sound of Silence: A Mathematical Philosophy

There is a sound that carries no vibration, a music made of absence, a rhythm born from the space between heartbeats. Silence is not emptiness—it is a canvas on which the universe paints its subtlest equations.

In the hush of a room, where clocks tick softly and thoughts wander, we hear the geometry of being. Each pause, each stillness, is a point plotted on the graph of experience. Between these points stretches an infinite line, a continuum where the seen and unseen converge. Silence, then, is not a void—it is a field of potential, a formula yet to be solved.

Mathematical philosophy teaches us to look beyond numbers and symbols, to find patterns in abstraction, to embrace the logic of imagination. Consider zero: the absence of quantity, yet the fulcrum on which all calculations balance. Silence, like zero, is paradoxically full; it holds every possibility, awaiting the mind that dares to observe it.

Fibonacci whispers in quiet moments. The spiral of thought, the curve of contemplation, grows outward from silence itself. Each reflective pause is a term in an eternal sequence, each breath a fractal, infinite in its depth. In silence, symmetry emerges—hidden ratios and harmonies that escape the noise of ordinary life.

Philosophers of mathematics, from Pythagoras to modern thinkers, have always understood that truth often lives in the gaps. A theorem proves itself not only in its conclusions but in the space left between steps. Similarly, silence proves itself not by what it contains, but by what it allows us to imagine.

To sit with silence is to engage in the most abstract of calculations: the arithmetic of thought, the algebra of emotion, the geometry of being. One begins to see patterns where none seem to exist, to hear melodies that only numbers can sing, to recognize the symmetry of one’s own consciousness reflected in the quiet.

So, let the noise of the world fade. Close your eyes and listen—not for sound, but for the structure beneath it. In the sound of silence lies a philosophy older than language, a theorem written in the spaces between stars, a proof that the universe itself breathes in rhythms of pause and possibility.

Silence is the ultimate equation: infinitely simple, infinitely profound, infinitely waiting for you to solve it.

Much love,

CoCash

By CoCash

Hey What Goodie boss,

Glad you came through to the spizzot”

Let’s walk through a timeline of Chinese mathematical philosophers, highlighting not just who they were, but the philosophical currents that ran through their work. I’ll blend history with their math-philosophy.

1. Early Foundations (c. 1000–200 BCE)

Texts & Figures: Zhou Bi Suan Jing (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven)

Philosophy: Numbers are more than tools—they express cosmic order. Shadows, circles, and right triangles weren’t just measurements; they were ways of understanding Heaven. Math was morality in action: precise calculation = moral discipline.

2. Classical Mathematicians (200–500 CE)

Liu Hui (c. 220–280 CE)

Annotated Nine Chapters on the Mathematical Art. Emphasized reasoning, rigor, and proportionality. Philosophy: Truth is discovered through careful thought; calculation mirrors moral and cosmic balance.

Zhang Heng (78–139 CE)

Astronomer and mathematician. Saw geometry as a reflection of the universe’s rhythm: round Heaven, square Earth. Philosophy: Numbers are poetry; mathematics is music of the cosmos.

Zu Chongzhi (429–500 CE)

Approximated π with astounding accuracy. Philosophy: Precision in mathematics cultivates the mind; numbers reveal hidden harmony of Heaven.

3. Neo-Confucian & Daoist Influences (1000–1300 CE)

Shen Kuo (1031–1095)

Invented ingenious measurement devices; explored geometry and astronomy. Philosophy: Observation + reasoning reveals underlying principles; math is the path to understanding the Dao.

Zhu Xi (1130–1200)

Not a mathematician per se, but influenced mathematical thought. Philosophy: Numbers and patterns reflect Li—the universal moral and structural order.

Qin Jiushao (c. 1202–1261)

Advanced polynomial equations. Philosophy: Calculation is not just pragmatic; it aligns human action with cosmic law.

4. Late Imperial & Pre-Modern Era (1300–1800 CE)

Mathematicians increasingly focused on algebra, combinatorics, and applied math. Philosophy: Even as math became more technical, scholars framed it as cultivating precision, patience, and understanding the hidden patterns of the universe.

5. Modern Chinese Mathematical Philosophers (1900–Present)

Hua Luogeng (1910–1985)

Pioneered number theory and combinatorial methods. Philosophy: Mathematical thinking is a moral and social practice; abstract reasoning strengthens character.

Wu Wenjun (1919–2017)

Algebraic topology and automated reasoning. Philosophy: The logic of mathematics mirrors the logic of the mind; automated proofs reveal deeper truths.

C.N. Yang (born 1922)

Nobel-winning physicist; reflected on symmetry and beauty. Philosophy: Mathematics is the language of nature, echoing Daoist balance and elegance.

🌌 The Thread That Binds

Across 2,000+ years, Chinese math philosophers share key ideas:

Cosmic Order: Math is a mirror of Heaven and Earth. Moral Discipline: Precision and rigor cultivate virtue. Harmony: Numbers and patterns express balance in nature and society. Integration of Art & Science: Calculation is intertwined with poetry, music, and philosophy. Imagination & Insight: Beyond computation, math reveals invisible structures of reality.

Much love,

CoCash

By CoCash

In ancient China, mathematics and philosophy were never really separate disciplines. Numbers were part of cosmology, harmony, and ethics — connected to how the universe was ordered.

Here’s a brief sense of the scope:

🌕 Classical Era (before 500 CE)

1. Zhou Bi Suan Jing authors (c. 1000–200 BCE)

This early text blends math with astronomy and moral cosmology — it treats geometry and shadow measurement as part of understanding Heaven’s will.

2. Liu Hui (c. 220–280 CE)

He wrote detailed commentaries on The Nine Chapters on the Mathematical Art, exploring logic, proportion, and harmony. His writing often feels like math-philosophy — deeply reflective on reasoning itself.

3. Zhang Heng (78–139 CE)

Astronomer, mathematician, and poet. He linked mathematical precision to cosmic rhythm — “the roundness of Heaven and squareness of Earth.”

4. Zu Chongzhi (429–500 CE)

Calculated π to seven decimal places — but also wrote about the metaphysical meaning of precision and the moral discipline it required.

☯️ Neo-Confucian and Daoist Mathematicians

5. Shen Kuo (1031–1095)

In Dream Pool Essays, he merges science, logic, and philosophy, describing how mathematics reveals “the principles that Heaven hides.”

6. Zhu Xi (1130–1200)

While not purely a mathematician, his Neo-Confucian philosophy inspired mathematical thinkers — he believed numbers mirrored the structure of Li (the universal order).

7. Qin Jiushao (c. 1202–1261)

Author of Mathematical Treatise in Nine Sections, working on polynomial equations. His preface connects calculation to moral virtue and cosmic insight.

🧠 Modern Era

8. Hua Luogeng (1910–1985)

A 20th-century mathematician who philosophized about “mathematical thinking” as a way of cultivating character and national consciousness.

9. Wu Wenjun (1919–2017)

Blended algebraic topology with a deep sense of Chinese logic and systematic reasoning — he even proposed a “philosophy of automated reasoning.”

10. C.N. Yang (born 1922)

Though best known for physics, his reflections on symmetry and mathematical beauty align closely with Daoist ideas of balance — truly a mathematical philosopher of modern times.

So depending on how we define math philosopher, there have been dozens, perhaps hundreds, throughout Chinese history — because the tradition never divorced mathematics from the art of living or the harmony of Heaven and Earth.

By CoCash (TikTok:@Hammertwo3)

Mathematics has one of the most sensual and secretive histories of any human invention — a language that began as counting pebbles and became a way to count galaxies. It’s the story of how symbols became desire, precision, and prophecy. Let’s move through its pulse, era by era.

1. The Ancient Spark

It began with rhythm. Before numbers, humans had patterns — the cycles of the moon, the beat of footsteps, the shape of the hunt. In ancient Sumer, people marked clay tablets to track grain and trade. Those marks — wedges and strokes — became the earliest recorded math around 3000 BCE. Egypt followed with geometry, quite literally “earth-measure,” born from the need to reclaim farmland after the Nile’s floods. Every pyramid was a love letter to symmetry and proportion.

2. The Greeks and the Idea of Proof

When math met philosophy in Greece, it became abstract — sacred. Thales, Pythagoras, Euclid — they didn’t just calculate; they meditated through logic. Pythagoras turned numbers into music, believing the universe itself sang in ratios. Euclid wrote The Elements, a geometry bible that ruled intellectual life for two thousand years. To them, mathematics wasn’t a tool — it was a temple.

3. India, Arabia, and the Zero Revolution

The most dangerous idea in history arrived quietly: zero. Indian mathematicians like Brahmagupta (7th century CE) defined it not as nothing, but as a position — a space that gives meaning to others. From India, this new system flowed to the Islamic world, where scholars in Baghdad’s House of Wisdom turned mathematics into art. Al-Khwarizmi, the father of algebra (from al-jabr, “reunion of broken parts”), gave us both the word “algorithm” and the mindset of symbolic reasoning.

4. The Renaissance Reawakening

As Europe rediscovered ancient texts, math became fashionable again — a weapon of explorers and architects. Fibonacci brought Arabic numerals to the West, making calculation fluid and fast. Artists like da Vinci and Brunelleschi used perspective, geometry, and proportion to sculpt space itself. Numbers were no longer cold—they painted, they seduced.

5. The Age of Calculus and Motion

By the 17th century, Newton and Leibniz turned math into motion. Calculus emerged — the language of change. It described the fall of apples and the orbits of planets, the smooth and the infinite. It was both scandal and enlightenment: two men fighting over who had first touched the infinite.

6. The Abstract Centuries

From the 1800s onward, math became more mysterious — and more seductive. Gauss, Riemann, and Noether explored non-Euclidean spaces, algebraic symmetries, and invisible dimensions. Math became less about numbers and more about structures, patterns, and logic itself.

7. The Digital and Quantum Eras

The 20th century turned math electric. Gödel showed that logic had limits. Turing transformed it into computation — the beginning of artificial minds. And in the quantum world, probability and uncertainty became the new geometry. Mathematics became the backstage language of everything: markets, codes, algorithms, desire.

8. The Present Moment

Now, in the 21st century, we stand in math’s newest evolution — data, machine learning, simulation. Equations no longer live on chalkboards; they move through our phones, through neural networks that learn and dream. We’re teaching math to imagine.

Much love,

CoCash